Mastering Addition with Regrouping: K to Grade 2 Journey

Learning addition with regrouping marks a significant milestone in Grade 1 as it introduces kids to the essential concept of place value initially. At this stage, many students still use counting methods for adding within teen numbers, which is appropriate for Kindergartners.

However, it's important for students to also begin practicing and mastering strategies such as decomposing both single-digit and teen numbers, making ten, and adding onto a ten.

Why? Because mastering these techniques lays a solid groundwork for understanding more advanced topics like addition with carrying larger whole numbers in Grades 1 and 2. As such, teaching how to add with regrouping really starts in Kindergarten using base ten blocks and in Grade 1 using a place value chart!

How to teach adding with regrouping

Regrouping in math refers to the practice of grouping numbers by place value (tens, hundreds, thousands, etc.) during addition. The process of teaching adding with regrouping involves helping students understand that they need to add each place value separately and progress to higher place values as needed.

This method becomes particularly useful for adding larger numbers efficiently. The process of adding 2 digit numbers with regrouping is the same as adding three digit numbers with regrouping or adding 4 digits with regrouping.

Breaking teen numbers: a foundation for understanding regrouping in Kindergarten

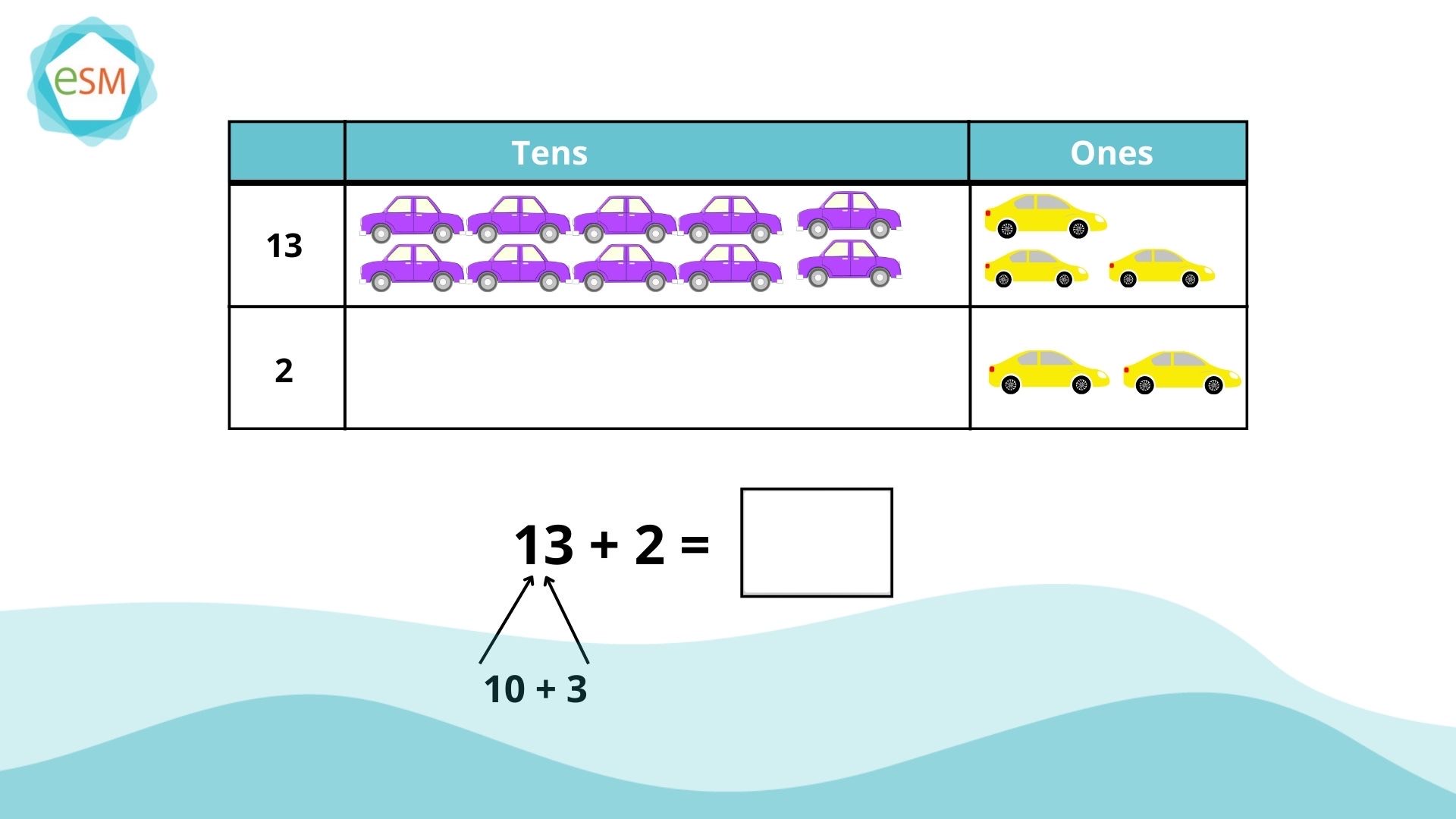
The foundation of understanding regrouping starts with teen numbers. In Kindergarten, for instance, when students encounter a number like 13 represented as one group of ten and 3 ones, many begin counting from one onwards (one, two, there, etc.). They may overlook that 13 can be understood as 10 + 3. This oversight can create a challenge for kids to develop number fluency and often sets apart students who excel from those who are facing challenges.

Watch how students study place value using the E-Singapore Math program. This concept is further reinforced using an interactive game in the same lesson.

Strategies for Success in First Grade

Practice Breaking Numbers

As shown in the video it’s beneficial to break teen numbers into ten and some more early in first grade. In 13 + 2, 13 is broken into 10 and 3. Then we add 3 ones and 2 ones separately to make 5. And then we add the 5 to the 10. While it's common for first-grade students to rely on counting to get the answer, they should also be encouraged to decompose teen numerals into a tens and ones, then perform the addition. This strategy fosters flexibility in dealing with teen numbers and helps develop a stronger sense of numbers.

Practice Making a Ten

When faced with the simple expression 6 + 7, many students may know the answer because they memorized it previously. However, when asked to add 6 to 27, some students struggle carrying over addition because they may not have fully grasped or mastered the concept of making a ten. That’s why early in Grade 1, consistent and effective strategy of teaching how to add with regrouping involves making a ten and then adding on.

The process of adding 6 to 7 is the same as adding two digits with regrouping. We can decompose 6 into 3 and 3. First, add 3 to 7 to make 10. Then, add the remaining 3 to the 10: 7 + 3 + 3 = 13.

Interactive Instruction: Exploring Regrouping with E-Singapore Math

In our E-Singapore Math Program, we utilize adding numbers with regrouping videos for kids to meticulously illustrate the whole process. Every step of the addition algorithm is vividly demonstrated and explained visually and verbally. For example, watch this adding with regrouping video:

The Case for Strategic Math Learning: Beyond Memorization

Some educators question why young kids should invest a significant amount of time learning addition with carrying using teen numbers. After all, most basic math facts can be memorized or derived through counting alone. However, teaching adding with regrouping requires that students already possess reliable problem-solving strategies over mere memorization, which can sometimes be unreliable.

Moreover, students who engage in adding with regrouping activities of teen numbers develop a robust understanding of math and tend to find it easier to handle multi digit numbers in the upper grades. Subsequently, this proficiency extends also to subtraction and then to multiplication, division, fractions and decimals.

Watch the next video, which shows adding with regrouping game using a place value chart. The video also demonstrates game for adding with regrouping using mental math strategies:

Embracing Doubles: A Simple Approach to Early Addition

We've noticed that children often grasp concepts more easily when presented in pairs. For young learners just beginning to understand addition, doubles are particularly natural. For instance, teaching 7 + 7 is typically simpler than teaching 7 + 8.

The initial step is acquaint students with doubles: 6 + 6 , 7 + 7, 8 + 8, 9 + 9.  The next step is to present additional facts derived from these doubles. For example: 6 + 7 is 1 more than 6 + 6, so 6 + 7 is 1 more than 12.

Strategies for Adding Three Numbers: Building Flexibility

When combining three numbers within 20, two primary cases should be taken into account.

Case 1: When two of the numbers sum up to ten. Such an example adding with regroup could be 7 + 3 + 4. Here students can use a number bond under 7 and 3 to make ten. Then adding the remaining number 4 results in the equation 10 + 4 = 14.

Case 2: When no combination of the numbers results in a sum of ten directly. In this situation, students must break down one of the numbers so that part of it can combine with another number to make ten. For example, in 3 + 8 + 9, students can decompose 8 into 1 and 7. Then, they can combine 1 with 9 make ten, resulting in 10 + 7 + 3= 20.

Since this concept may be new and challenging for first grade students, many children initially rely on counting. Nevertheless, based on our experience, we've discovered that although not all first graders immediately grasp this concept, it's vital to introduce this adaptability early to show that counting isn't the sole approach.

Understanding Regrouping in Grade 2: Adding Three-Digit Numbers

Let's consider the example of adding 237 and 148 using the regrouping method.

First, we write the equation in column form:

If we start by adding the ones column (7 + 8), we get 15. However, we can only write one digit in the ones place, so regrouping becomes necessary. In regrouping, we exchange 10 ones for 1 ten.

So, 7 + 8 equals 15, which we can split into 'one group of ten' and 'five ones'. We write 5 in the ones column and carry over 1 ten to the tens column.

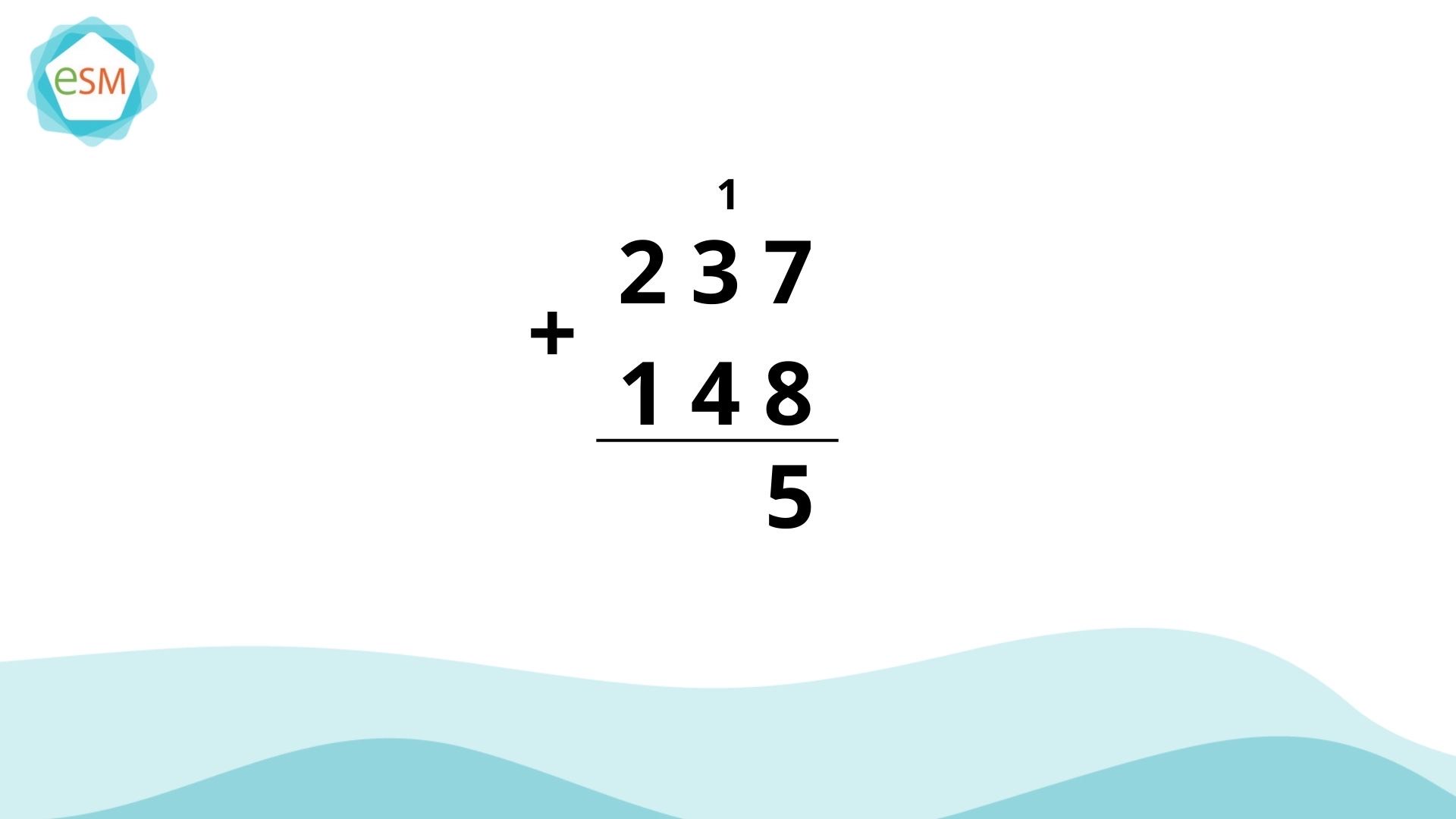
Now, we add the tens: 1 ten + 3 tens + 4 tens = 8 tens.

Then, we add hundreds: 2 hundreds + 1 hundred = 3 hundreds.

Therefore, the sum of 237 and 148 is 385. Watch 3 digit adding with regrouping in this video:

In conclusion, the concept of regrouping in early math education is foundational for developing strong number sense and problem-solving skills. Starting from understanding place value and decomposing numbers in simple addition, such as making ten, to applying regrouping strategies in more complex calculations with multi-digit numbers, students build essential skills that extend beyond basic arithmetic.
Through interactive methods like those in the E-Singapore Math Program, children gain a deeper understanding of math, paving the way for future academic achievement and a lifelong appreciation for the power of numbers.